Charles L. Webber, Jr., Ph.D.

Professor Emeritus
Department of Cell and Molecular Physiology
Stritch School of Medicine
Loyola University Chicago
Health Sciences Division
2160 South First Avenue
Maywood, IL 60153 USA

RECURRENCE QUANTIFICATION ANALYSIS (RQA) is a powerful analytical tool developed over the last decade for the study of nonlinear dynamical systems. RQA is the necessary extension of recurrence plot analysis (RPA), a more qualitative tool. Since RQA methodology is independent of limiting constraints such as data set size, data stationarity, and assumptions regarding statistical distributions of data, RQA seems ideally suited for physiological systems characterized by non-homeostatic transients, state changes, and noise from within and without the organism or process. Mathematical details and the physiological utility of RQA are described in numerous papers with Joseph P. Zbilut, Ph.D., DNSc of Rush University (deceased Jan. 10, 2009).

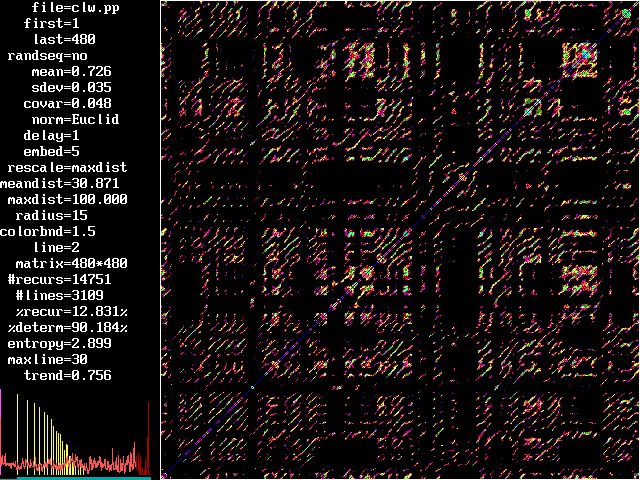
RECURRENCE PLOTS AND QUANTIFICATION OF RECURRENCES are illustrated below for data derived from a normal human electrocardiogram (continuous flow). The input data for each plot consist of the same 480 consecutive RR intervals (discrete map) embedded in 5 dimensions. A local recurrence plot (left) is generated by keeping the radius low (15% of maxdist), allowing recurrences to occur only in near neighborhoods. A global recurrence plot (right) is generated by saturating the radius (100% of maxdist), allowing for all possible recurrences. The various colors reflect different Euclidean distances between trajectories and are analogous to geographical relief maps. Five RQA variables are computed (%recurrence, %determinism, information entropy, maximum diagonal line length, state trend) which have relevancy as nonlinear markers of changes in dynamical systems and physiological states. For specific details regarding RQA implementation (easy) and RQA interpretation (difficult), see our publications (above) and free software release (below).

LOCAL RECURRENCE PLOT

GLOBAL RECURRENCE PLOT

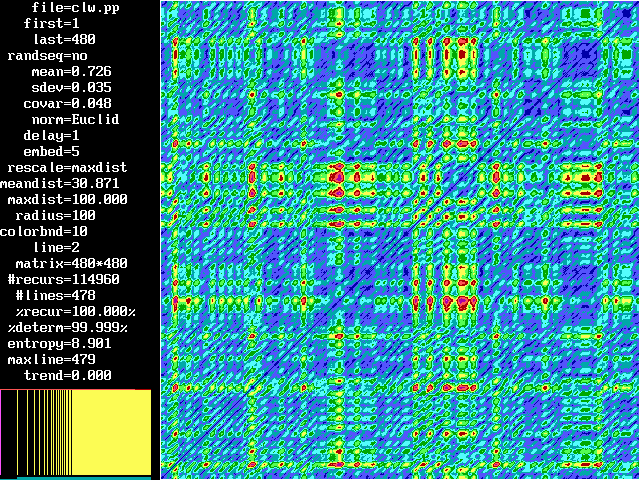RQA SOFTWARE that generates images like those above and other RQA utilities are embedded within downloadable ZIP file Download RQA161. The current distribution version of this software includes 57 executable RQA programs, 11 utility programs, 21 example data files, and an explanatory readme file READ2021.PDF and key monograph RQA_NLD.PDF.

Please contact Dr. Webber directly (phone, electronic mail, snail mail) with any questions regarding research applications of these RQA programs. cwebber@luc.edu

Created: August 22, 1996
Revised: August 12, 2021

• Webber, C.L., Jr. (1974).  Quantitative Analysis of Respiratory Cell Activity. Chicago: Ph.D. Dissertation, Loyola University Chicago.
  http://ecommons.luc.edu/cgi/viewcontent.cgi?article=2432&context=luc_diss
• Webber, C.L., Jr. (1991). Rhythmogenesis of deterministic breathing patterns. In: Rhythms in Physiological Systems, H. Haken and H.-P. Koepchen (eds.). Springer-Verlag, Berlin, pp. 171-191.
• Zbilut, J.P., Webber, C.L., Jr. (1992). Embeddings and delays as derived from quantification of recurrence plots. Phys. Lett . A 171: 199-203.
• Webber, C.L., Jr., Zbilut, J.P. (1994). Dynamical assessment of physiological systems and states using recurrence plot strategies. J. Appl. Physiol. 76: 965-973.
• Webber, C.L., Jr., Schmidt, M.A., Walsh, J.M. (1995). Influence of isometric loading on biceps EMG dynamics as assessed by linear and nonlinear tools. J. Appl. Physiol. 78: 814-822.
• Webber, C.L., Jr., Zbilut, J.P. (1996). Assessing deterministic structures in physiological systems using recurrence plot strategies. In: Bioengineering Approaches to Pulmonary Physiology and Medicine. M.C.K. Khoo (ed.) Plenum Press, New York, Chapter 8, pp 137-148.
• Trulla, L.L, Giuliani, A., Zbilut, J.P., Webber, C.L., Jr. (1996). Recurrence quantification analysis of the logistic equation with transients. Phys. Lett. A 223: 255-26.
• Zbilut, J.P., Giuliani, A., Webber, C.L., Jr. (1998). Recurrence quantification analysis and principle components in the detection of short complex signals. Phys. Lett. A 237: 131-135.
• Zbilut, J.P., Webber, C.L., Jr (1998). Quantification of heart rate variability using methods derived from nonlinear dynamics. In: Analysis and Assessment of Cardiovascular Function. G. Drzewiecki and J.K.-J. Li (eds.). Springer Verlag, New York, Chapter 19, pp. 324-334.
• Zbilut, J.P., Giuliani, A., Webber, C.L. Jr., Colosimo, A. (1998). Recurrence quantification analysis in structure-function relationships of proteins: an overview of a general methodology applied to the case of TEM-1 beta-lactamase. Protein Engin. 11: 87-93.
• Zbilut, J.P., Giuliani, A., Webber, C.L., Jr. (1998). Detecting deterministic signals in exceptionally noisy environments using cross-recurrence quantification. Physics Lett. A 246: 122-128.
• Webber, C.L., Jr., Zbilut, J.P. (1998). Recurrent structuring of dynamical and spatial systems. In: Complexity in the Living: A Modelistic Approach. A. Colosimo (ed.). Proc. Int. Meet., Feb. 1997, University of Rome "La Sapienza," pp. 101-133.
• Manetti, C., Ceruso, M.-A., Giuliani, A., Webber, C.L., Jr., Zbilut, J.P. (1999). Recurrence quantification analysis as a tool for the characterization of molecular dynamics sumilations. Physical Rev. E. 59: 992-998.
• Manetti, C., Ceruso, M.-A., Giuliani, A., Webber, C.L., Jr., Zbilut, J.P. (1999). Recurrence quantification analysis in molecular dynamics. Annl. N.Y. Acad. Sci. 879: 258-266.
• Orsucci, F., Walter, K., Giuliani, A., Webber, C.L., Jr., Zbilut, J.P (1999). Orthographic structuring of human speech and texts: linguistic application of recurrence quantification analysis. Int. J. Chaos Theory Appl. 4: 21-28.
• Zbilut, J.P., Colosimo, A., Webber, C.L., Jr., Giuliani A. (2000). The role of hydrophobicity patterns in prion folding as revealed by recurrence quantification analysis of primary structures. Protein Eng. 13: 99-104.
• Ikegawa, S., Shinohara, M., Fukunaga, T., Zbilut, J.P., Webber, C.L., Jr. (2000). Nonlinear time-course of lumbar muscle fatigue using recurrence quantifications. Biol. Cybernetics 82: 373-382.
• Zbilut, J.P., Hu, Z., Webber, C.L., Jr. (2000). Singularities of the heart beat as demonstrated by recurrence quantification analysis. Proc. Eng. Med. Biol. Soc. CD ROM.
• Zbilut, J.P., Giuliani, A., and Webber, C.L., Jr. (2000). Recurrence quantification analysis as an empirical test to distinguish deterministic versus random number series. Phys. Lett. A 267: 174-178.
• Thomasson, N., Hoeppner, T.J., Webber, C.L., Jr., and Zbilut, J.P. (2001). Recurrence quantification in epileptic EEG's. Phys. Lett. A 279: 94-101.
• Manetti, C., Giuliani, A., Ceruso, M.-A., Cannistraro, S., Webber, C.L., Jr., Zbilut, J.P. (2001). Recurrence analysis of hydration effects on nonlinear protein dynamics: multiplicative scaling and additive processes. Phys. Lett. A 281: 317-323.
• Webber, C.L., Jr., Giuliani, A., Zbilut, J.P., Colosimo, A. (2001). Elucidating protein secondary structures using alpha-carbon recurrence quantifications. Protein: Struct. Funct. Gen. 44: 292-303.
• Giuliani, A., Colafranceschi, M., Webber, C.L., Jr., Zbilut, J.P. (2001). A complexity score derived from principle components analysis of nonlinear order measures. Physica A 301:567-588.
• Zbilut, J.P., Sirabella, P., Giuliani, A., Manetti, C., Colosimo, A., Webber, C.L., Jr. (2002). Review of nonlinear analysis of proteins through recurrence quantification. Cell. Biochem. Biophys. 36: 67-87.
• Zbilut, J.P., Thomasson, N., Webber, C.L., Jr. (2002). Recurrence quantification analysis as a tool for nonlinear exploration of nonstationary cardiac signals. Med. Engin. Physics 24: 53-60.
• Giuliani, A., Benigni, R., Zbilut, J.P., Webber, C.L., Jr., Sirabella, P., Colosimo, A. (2002). Nonlinear signal analysis methods in the elucidation of protein sequence/structure relationships. Chem. Rev. 102: 1471-1491.
• Thomasson, N., Webber, C.L., Jr., Zbilut, J.P. (2002). Application of recurrence quantification analysis to EEG signals. Int. J. Comp. Appl. 9: 1-6.
• Shockley, K., Buttwill, M., Zbilut, J.P., Webber, C.L., Jr. (2002). Cross recurrence quantification of coupled oscillators. Phys. Lett. 305: 59-69.
• Zbilut, J.P., Colosimo, A., Conti, F., Colafranceschi, M., Manetti, C., Valerio, M.-C., Webber, C.L., Jr., Giuliani, A. (2003). Protein aggratation/folding: The role of deterministic singularities of sequence hydrophobicity as determined by nonlinear signal analysis of acylphosphatase and A-beta(1-40). Biophysical J. 85: 3544-3557.
• Liu, Y, Kankaanpaa, M., Zbilut, J., Webber, C.L., Jr. (2004). EMG recurrence quantifications in dynamic exercise. Biol. Cybernetics 90: 337-348.
• Zbilut, J.P., Mitchell, J.C., Giuliano, A., Colosino, A., Marwan, N., Colafranceschi, M., Webber, C.L., Jr. (2004). Aggregation propensity of proteins quantified by hydrophobicity paterns and net charge. In: Complexity in the living: A problem-oriented approach. A. Colosimo, ed., Proc. Int. Meet., Sept. 2004, University of Rome "La Sapienza," pp. 139-157.
• Zbilut, J.P., Giuliani, A., Colosimo, A., Mitchell, J.C., Colafranceschi, M., Marwan., N., Webber, C.L., Jr. (2004). Charge and hydrophobicity patterning along the sequence predicts the folding mechanism and aggregation of proteins: a computational approach. J. Proteome Res. 3:1243-1253.
• Zbilut, J.P., Scheibel, T., Huemmerich, D., Webber, C.L., Jr., Colafranceschi, M., Giuliani, A. (2005). Spatial stochastic resonance in protein hydrophobicity. Phys. Lett. A 346:33-41.
• Webber, C.L., Jr., Zbilut, J.P. (2005). Recurrence quantification analysis of nonlinear dynamical systems. In: Tutorials in contemporary nonlinear methods for the behavioral sciences, (Chapter 2, pp. 26-94), M.A. Riley, G. Van Orden, eds. Retrieved December 1, 2004 http://www.nsf.gov/sbe/bcs/pac/nmbs/nmbs.pdf
• Webber, C.L., Jr. (2005). The meaning and measurement of physiological variability? Crit. Care Med. 33: 677-678.
• Webber, C.L., Jr., Zbilut, J.P. (2006). Ventilatory pattern variability. In: Wiley Encyclopedia of Biomedical Engineering. M. Akay, ed. John Wiley & Sons, Hoboken, DOI: 10.1002/9780471740360.ebs1260
• Zbilut, J.P., Webber, C.L., Jr. (2006). Recurrence quantification analysis. In: Wiley Encyclopedia of Biomedical Engineering. M. Akay, ed. John Wiley & Sons, Hoboken, DOI: 10.1002/9780471740360.edb1355
• Orsucci, F., Giuliani, A., Webber, C.L., Jr., Zbilut, J., Fonagy, P., Mazza, M. (2006). Combinatorics and synchronization in natural semiotics. Physica A 361: 665-676.
• Schumacher, A.M., Zbilut, J.P., Webber, C.L., Jr., Schwertz, D.W., Piano, M.R. (2006). Detection of cardiac variability in the isolated rat heart. Physiol Meth. Nrusing Res. 8: 55-66.
• Fisher, M.A., Chawla, J., Webber, C.L., Jr. (2006). Deterministic recurrences of sequential F-wave latencies. Neurology, Neurophysiology, and Neuroscience 8:1-2. http://www.neurojournal.com/article/view/496/553
• Zbilut, J.P., Chua, G.H., Krishnan, A., Bossa, C., Rother, K., Webber, C.L., Jr., Giuliani, A. (2007). A topologically related singularity suggests a maximum preferred size in protein domains. Proteins: Struct., Funct., Bioinformatics 66:621-629.
• Vlahogianni, E.I., Webber, C.L., Jr., Geroliminis, N., Skabardonis, A. (2007). Statistical characteristics of transitional queue conditions in signalized arterials. Transportation Res. C 15 392-403.
• Sarkar, A., Webber, C.L., Jr., Batata, P., Mukherjeea, P. (2007). Recurrence analysis of the Portevin-Le Chatelier effect. Phys. Lett. A. http://dx.doi.org/10.1016/j.physleta.207.08.055
• Webber, C.L., Jr., Zbilut, J.P. (2007). Recurrence quantifications: Feature extractions from recurrence plots. Int. J. Bifurcation Chaos 17:3467-3475.
• Zbilut, J.P., Webber, C.L., Jr. (2007). Recurrence quantification analysis: Introduction and historical context. Int. J. Bifurcation Chaos 17:3477-3481.
• Carrubba, S., Frilot, C., Chesson, A.L., Jr., Webber, C.L., Jr., Zbilut, J.P., Marino, A.A. (2008) Magnetosensory evoked potentials: Consistent nonlinear phenomena. Neuroscience Res. 60: 95-105.
• Zbilut, J.P., Webber, C.L., Jr. (2008). Laminar recurrences, maxline, unstable singularities and biological dynamics. European Physics J. Special Topics 164:55-65.
• Webber, C.L., Jr., Marwan, N., Facchiani, A. Giuliani, A. (2009). Simpler methods do it better: Success of recurrence quantification analysis as a general purpose data analysis tool. Physics Lett. A http://dx.doi.org/10.1016/j.physleta.2009.08.052
• Keller, A.J., Webber, C.L., Jr. (2010). Classifying musical genre using recurrence strategies. Chaos Complexity Lett. 5(1): 1-15.
• Kulkarni, A., Marwan, N., PArrott, L., Proulx, R., Webber, C.L., Jr. (2011).Recurrence plots at the crossroad between theory and application. Int. J. Bifurcation Chaos 21:997-1001.
• Webber, C.L., Jr., Hu, Z., Akar, J. (2011). Unstable cardiac singularities may lead to atrial fibrillation. Int. J. Bifurcation Chaos 21:1141-1151.
• Kulkarni, A., Marwan, N., Parrott, L., Proulx, R., Webber, C.L., Jr. (2011). Recurrence plots at the crossroad between theory and application. Int. J. Bifurcation Chaos 21: 997-1001.
• Webber, C.L., Jr. (2012). Nonlinear Cardiac Dynamics. In: Current Issues and Recent Advances in Pacemaker Theory. A. Roka, ed. InTech on-line publisher, ISBM 979-953-307-839-6. Chapt. 11, pp. 233-246.
• Webber, C.L., Jr. (2013) Recurrence Quantification of Fractal Structures. In: Fractal Analyses: Statistical and Methodological Innovations and Berst Practices. J. Holden, M. Riley, J. Gao, K. Torre, eds. Frontiers in Fractal Physiology, Vol. 3, Art. 382, pp. 1-11.
• Keller, A.J., Webber, C.L., Jr. (2013). Classifying musical genre using recurrence strategies. In: Chaos and Complexity Research Compendium. F. Orsucci amd N. Sala, eds. Nova Publishers, ISBN 978-1-62081-872-5. Chapt. 10. pp. 153-168.
• Marwan, N., Riley, M., Giuliani, S., Webber, C.L., Jr. editors (2014).Translatioinal Recurrence: From Mathematical Theory to Real-World Applications. Springer Proceedings in Mathematics & Statistics, Vol. 3. Springer International Publishing, Cham, Switzerland. http://dx.doi.org/10.1007/978-3-319-09531-8
• Webber, C.L., Jr., Marwan, N. editors (2015).Recurrence Quantification Analysis: Theory and Best Practices. Springer Series: Understanding Complex Systems. Springer International Publishing, Cham, Switzerland. http://dx.doi.org/10.1007/978-3-319-07155-8
• Marwan, N., Webber, C.L., Jr. (2015). Mathematical and computational foundations of recurrence quantifications. In:Recurrence Quantification Analysis: Theory and Best Practices. Springer Series: Understanding Complex Systmes. Springer International Publishing, Cham, Switzerland, pp. 1-41.
• Webber, C.L., Jr., Ioana, C., Marwan, N., Editors (2016).  Recurrence Plots and Their Quantifications: Expanding Horizons. Proceedings of the 6th International Symposium on Recurrence Plots, Grenoble, France, 17-19 June 2015.  Springer Proceedings in Physics. Vol. 180.  Springer International Publishing, Cham Switzerland. http://dx.doi.org/10.1007/978-3-319-29922-8
• Webber, C.L., Jr. (2016).  Splayed Recurrence Analysis of Iterated Dynamical Systems. In: Recurrence Plots and Their Quantifications: Expanding Horizons.  Springer Series: Springer Proceedings in Physics, Vol. 180. Webber, C.L., Jr., Ioana, C., Marwan, N., eds.. Springer International Publishing, Cham Switzerland, pp. 137-153
• Hummel, J.P., Baher, A., Buck, B., Fanarjian, M., Webber, C.L., Jr., Akar J.G, (2017). A method for quantifying patterns of local wavefront direction during atrial fibrillation.  Computers Biol. Med. 89: 497-504.
• Marwan, N., Webber, C.L., Jr., Mscau, E.N., Viana, R.L. (2018). Introduction to focus issue: Recurrence quantification analysis for understanding complex systems.   Seventh International Symposium on Recurrence Plots, Sao Paulo, Brazil. Chaos 28. https://aip.scitation.org/doi/10.1063/1.5050929
• Hummel, J.P., Akar, J.G., Baher, A., Webber, C.L., Jr. (2018). New skip parameter to facilitate recurrence quantification of signals comprised of multiple components.   Seventh International Symposium on Recurrence Plots, Sao Paulo, Brazil. Chaos 28. https://aip.scitation.org/doi/full/10.1063/1.5024845
• Baher, A., Buck, B., Fanarjian, M., Mounsey, J.P., Gehi A., Chung, E., Akar, F.G., Webber, C.L., Jr., Akar, J.G., Hummel, J.P. (2019). Recurrence quantification analysis of complex‐fractionated electrograms differentiates active and passive sites during atrial fibrillation. J Cardiovasc Electrophysiol. 30:2229–2238. DOI: 10.1111/jce.14161.

P: (708) 638-7497
E: cwebber@luc.edu